The Maya Calendar – Part 6 – Numbers and Mathematics of the Maya – the Vigesimal System
This post “The Maya Calendar” is an excerpt of the 2nd edition of my book “The Maya Sites – Hidden Treasures of the Rain Forest”, a travel guide to the most important Maya sites on the Yucatán peninsula – in México and Guatemala. The 2nd edition will be published as print and ebook in spring 2018.
I split this article into seven parts:
- The Maya calendar – Part 1 – Introduction
- The Maya calendar – Part 2 – Haab, the Solar Year
- The Maya calendar – Part 3 – Tzolkin, the Sacred Calendar
- The Maya calendar – Part 4 – The Calendar Round
- The Maya calendar – Part 5 – The Long Count
- The Maya calendar – Part 6 – The Numbers and the Vigesimal System <<< You are here
- The Maya calendar – Part 7 – Dates and Numbers in the Inscriptions
Numbers and mathematics at the ancient Maya
Before we turn now to the presentation of the date in the inscriptions, I would like to briefly present the numbers and explain some of the calculation rules used by the Maya. No date can do without numbers.
As we have already seen in the introduction to the calendar, the ancient Maya were meticulous arithmetic artists. Dates were common in the inscriptions, but also distance numbers between two days to indicate a previous date were interspersed into the texts.
In the counting that underlies the Haab and Tzolkin calendar, you’ve already seen that the Maya used 20 numbers to determine the days. Mostly 0 to 19. If that surprised you, here is the explanation:
The Maya had no decimal system with tens, hundreds and thousands like us. Their system was vigesimal….. which means it was based on the number 20 as opposed to decimal, which is based on the number 10.
In fact, they not only used their ten fingers to count them but also used additionally their toes. A vigesimal system may seem unusual to us, but vigesimal seems to have been widespread in Europe too.
Such “base 20 numeral systems” were not only known in the more exotic European cultures, such as the Basques and Scots. Also in the languages of Slovenes, Danes, Georgians, Welsh, Albanians or Irish there are at least remnants of this number system.
And anyone who was allowed to learn French at school will remember the confusing quatre-vingt-dix-neuf (twenty-four-ten-nine), which expresses the number 99.
Here is how: (4×20)+10+9
Evil tongues claim that vigesimal systems were widespread mainly in barefoot cultures because they had made it easier for them to include their ten toes in the calculation system.
The presentation of the numbers
Let us first consider the representation of the numbers as they are handed down in the Codices and as they can be found in many inscriptions.
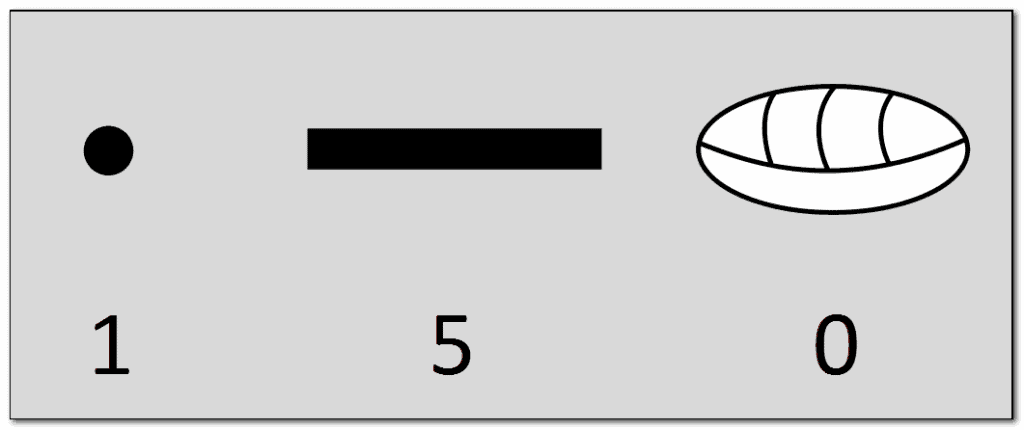
You will find 3 number symbols to express numbers. A dot has the value 1, a dash has the value 5 and for the 0 the Maya used the symbol of a shell.
In the inscriptions, it was customary to use so-called head signs for special numbers in addition to this dot-dash notation. The number 10 was expressed by the image of a skull. Later I will explain how numbers were noted in the inscriptions. Let’s take a closer look to the way of counting first.
The dot-dash notation works similarly to the beer coaster notation popular in German beer gardens. In this case, each beer is counted with a vertical line. The fifth beer, however, is represented by a horizontal line that crosses the first 4 lines. Then the waiter begins with a new group of dashes until he reaches 5. On the basis of this notation, the guests and the host are able to calculate the beverage costs correctly even at an advanced hour and under considerable alcohol influence.
The Maya did the same thing.
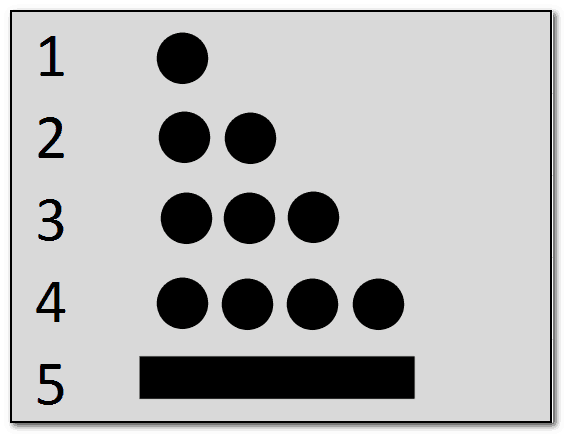
With 1 to 4 points, the numbers 1 to 4 were expressed. For the number 5, they used a line. It should be noted that in inscriptions the number symbols could also be rotated by 90 degrees.
Once the five had been reached, additional points were added. Here the number 8:
To express the number 10, two lines were used again:
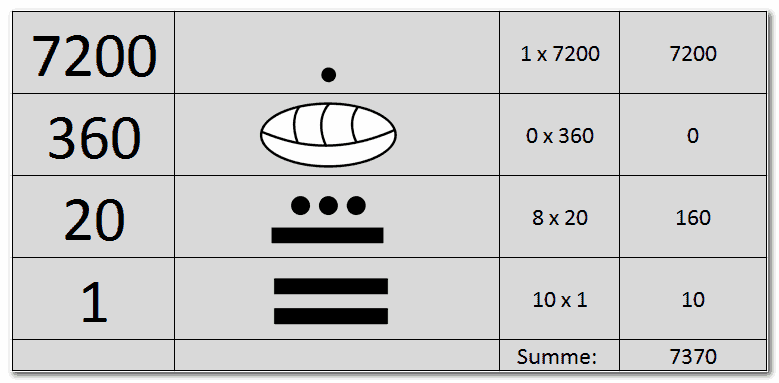
Numbers larger than twenty can also be recorded in this way. For this purpose, as with us, additional positions are used for the larger units.
In our decimal system, the number 312 is made from right to left out of two ones at first, a ten at second and 3 hundred at third place.
So:
3×100 = 300
1 x 10 = 10
2 x 1 = 2
In total: 312
The Maya also used a system of positional notation. However, since it is a vigesimal system, there are other values and positions in incremental counting. Mathematics speak of digits and numerals.
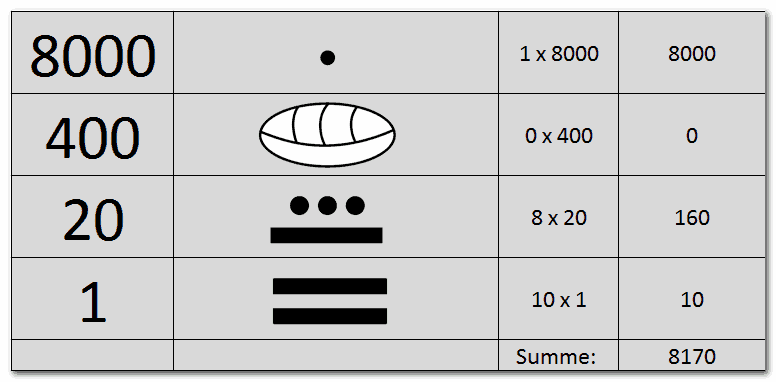
The place-value notation of the Maya was such that the smaller units lay below, the larger ones above them followed. Instead of going from right to left, they wrote their numbers from bottom to top.
The first digit was used to express the one and additionally the numbers 10 to 19, the second digit to denote the 20’s, the third digit to denote the 400’s and so on, each 20 times.
The following figure shows an example. By adding further digits you can display numbers of any size.
As we had already seen above in the description of the long count, the calendar systems always counted from 0 to 19. But there is an exception for the time unit Tun ( a solar year) for which only numbers from 0 to 17 were valid. Therefore, numbers showing a calendar date would be calculated slightly different than in simple counting.
Here is the corresponding table:
The representation of the numbers in the inscriptions
In addition to the dot-dash notation, the Maya used a whole series of head glyphs to represent their numbers. There are also illustrations for zero, which differ from the simple shell of dot notation.
The following tables are the most common headers for the numbers 0 – 20, denoted in the Mayan languages Mayathan and Cholan:
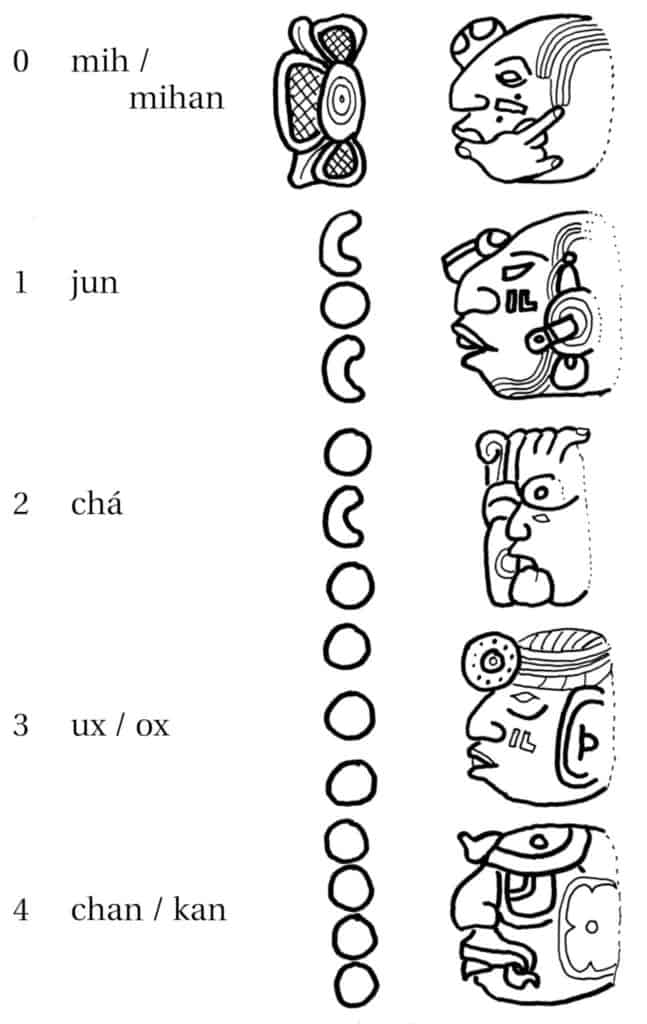
The Maya Calendar: The numbers 0 – 4 – mih/mihan,jun,cha’,ux/ox, chan/kan, ho
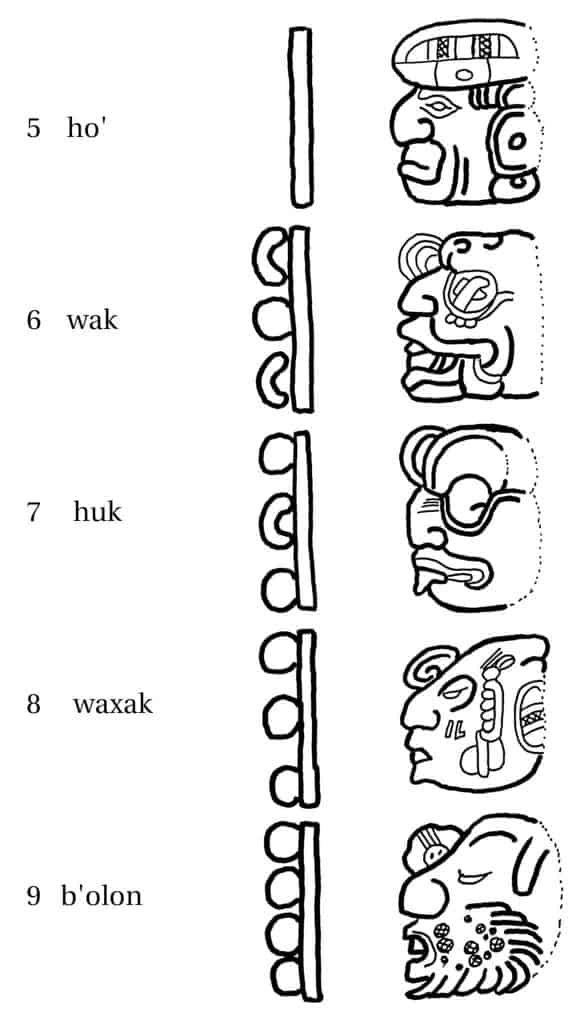
The Maya calendar Numbers 5-9 – ho’, wak, huk, waxak, bolon
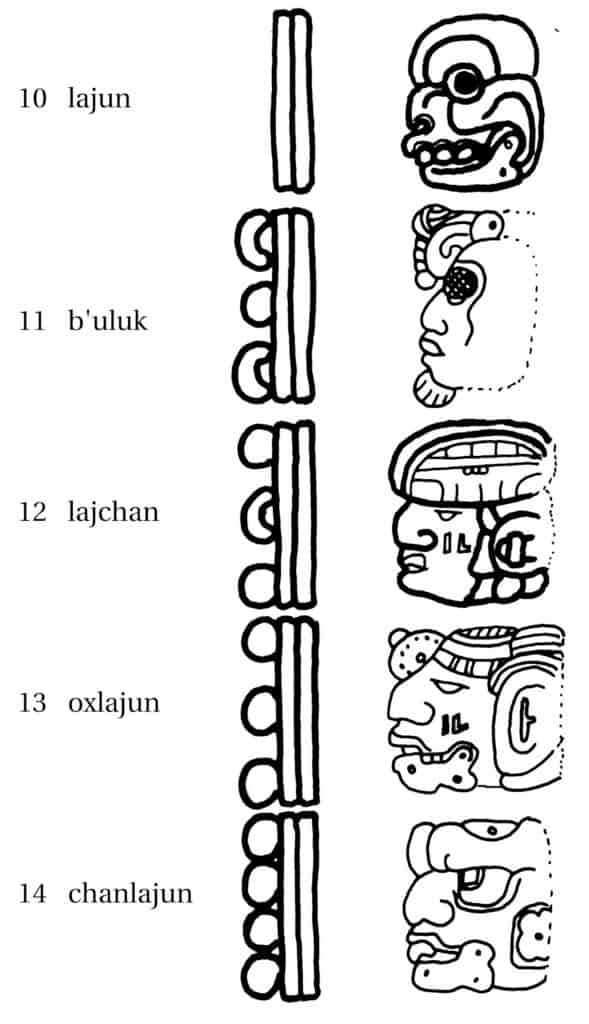
The Maya Calendar – Numbers 10 -14 – lajun, buluch/buluk, lajunchan, uxlajun/oxlajun, chanlajun
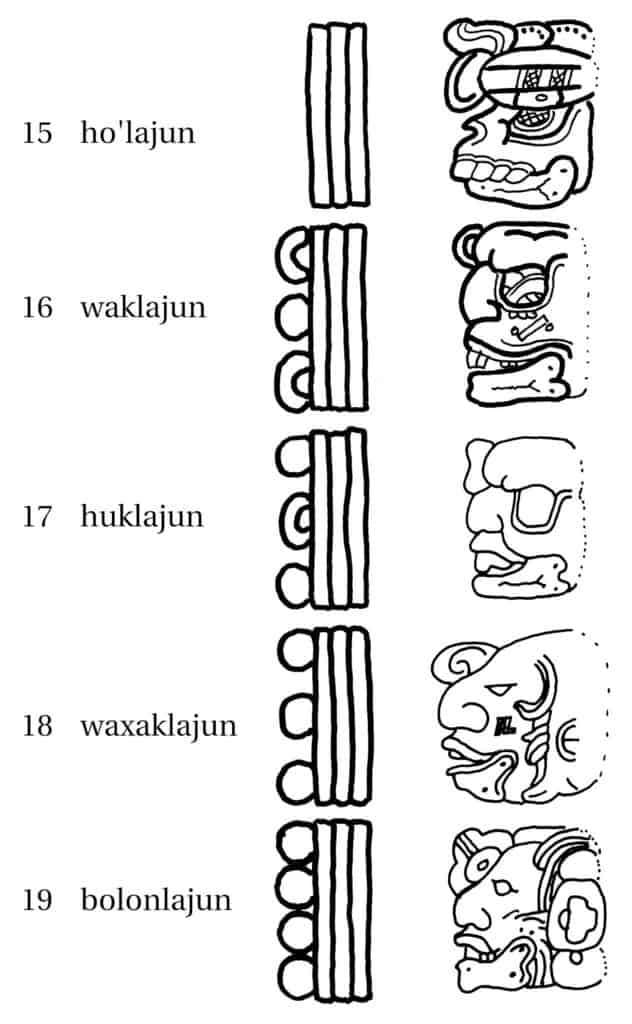
The Maya Calendar – Numbers 15-19 – ho’lajun, waklajun, huklajun, waxaklajun, bolonlajun
Now we basically have all the essential information together, so that we can deal with the actual date inscriptions carved in stone, as they were left by the Maya.
>>> Continue with: The Maya calendar – Part 7 – Dates and Numbers in the Inscriptions